Suppose you take on a loan for P Rupees, the tenure of the loan is n months (for example, n=240 for a 20-year loan), the monthly rate of interest is r (usually calculated by dividing the annual rate of interest quoted by the bank by 12, the number of months in a year, and dividing that by 100 as the rate is usually quoted as a percentage) and E Rupees is the EMI you have to pay every month. Let us use Pi to denote the amount you still owe to the bank at the end of the i-th month. At the very beginning of the tenure, i=0 and P0=P, the principal amount you took on as a loan.
At the end of the first month, you owe the bank the original amount P, the interest accrued at the end of the month r×P and you pay back E. In other words:
P1 = P + r×P – E
or to rewrite it slightly differently:
P1 = P×(1 + r) – E
Similarly, at the end of the second month the amount you still owe to the bank is:
P2 = P1×(1 + r) – E
or substituting the value of P1 we calculated earlier:
P2 = (P×(1 + r) – E)×(1 + r) – E
and once again expanding it and rewriting it slightly differently:
P2 = P×(1 + r)2 – E×((1 + r) + 1)
where "xy" denotes "x raised to the power y" or "x multiplied by itself y times". To make this look slightly simpler, we substitute "(1 + r)" by "t" and now it looks like this:
P2 = P×t2 – E×(1 + t)
Continuing in this fashion and calculating P3, P4, etc. we quickly see that Pi is given by:
Pi = P×ti – E×(1 + t + t2 + … + ti-1)
At the end of n months (that is, at the end of the tenure of the loan), the total amount you owe to the bank should have become zero. In other words, Pn=0. This implies that:
Pn = P×tn – E×(1 + t + t2 + … + tn-1) = 0
which means that:
P×tn = E×(1 + t + t2 + … + tn-1)
We can simplify this further by noticing that we have a geometric series of n terms here with a common ratio of t and a scale factor of 1. The sum of such a series is given by "(tn – 1)/(t – 1)", which we substitute in the above equation to yield:
P×tn = E×(tn – 1)/(t – 1)
which can be rewritten as:
E = P×tn×(t – 1)/(tn – 1)
which can again be rewritten by substituting the value of t back as "(1 + r)" as:
E = P×r×(1 + r)n/((1 + r)n – 1)
and this is the formula for calculating your EMI. This formula can also be rendered more clearly as:
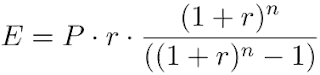
Suppose you take a loan from a bank of 10,00,000 Rupees for 15 years at 8.5% annual rate of interest calculated on a monthly rest basis. In that case, P = 10,00,000, n = 15×12 = 180 and r = (8.5/12)/100 = 0.0070833333. Putting these values into the formula given above gives us E = 9847.40 (approximately).
When you write a programme to calculate your EMI using the formula given above, be careful to structure your computations to accommodate loss of precision and rounding errors. For more information, read "What Every Computer Scientist Should Know About Floating-Point Arithmetic" (PDF) by David Goldberg or section 4.2, "Floating Point Arithmetic", in "The Art of Computer Programming, Volume 2: Seminumerical Algorithms" (3rd Edition) by Donald Knuth.
Source: rmathew: Calculating EMIs